Floating Point Numbers
In C++, floating point numbers can be represented in two data types; float and double
Float
1 sign bit + 8 bits for exponent + 23 bits for significant values
Double
1 sign bit + 11 bits for exponent + 52 bits for significant values
Steps for IEEE 754 single/double representation
- Convert floating number to binary number
- ex) 123.75
- first, convert 123 into two’s complement -> 1111011
- convert .75 into two’s complement – multiply .75 by 2 -> 1.5 remainder 1 – subtract 1 from 1.5, 0.5 * 2 -> 1.0 remainder 1 – (this process needs to be repeated until we end up with 0 or a cycle) – -> 11
- so all together 123.75 becomes 1111011.11
- Convert binary number into normalized form
- 1111011.11 -> 1.11101111 * 2^6
- Convert number in normalized form into IEEE 754 single representation
- The first bit is sign bit; 0 when positive and 1 and negative
- The second section is 8bit exponent – For the exponent, we have 6 – We need to add bias(2 ^ (n-1) - 1) + to our exponent – -> 127 + 6 -> 133 -> 10000101
- The last section is 23 bit significant values – because it needs to store significant values, the very first value will always be 1 – and therefore, we don’t need to store it -> 1110 1111 0000 0000 0000 0
Pictorial Explanation
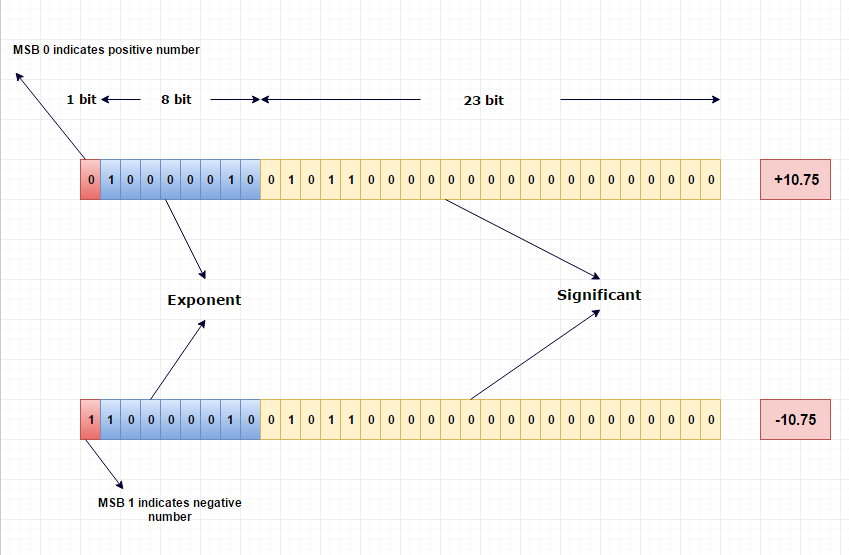
Why bias is used
- exponent section consists of 8 bits
- if we had the first bit as sign bit that we are left with 7bits
- which means the minimum number we can represent 128 numbers each for pos and neg – one problem with this is neg:[-127: 0] pos:[0: 127] which means we have 2 different representations for 0 – therfore, we can rearrange the ranges and make neg: [-127: 0] pos: [1: 128] – because the minimum number we can have is -127, we can make all the possible numbers positive if we set bias to 127
- So by using bias, represent everynumber as positive numbers so we can just store is as unsigned number
- and makes comparison easier
Precision / When to use double over float and vice versa
- no of sig bits of float is 23 bits -> 8388608 -> 7 decimal digits
- no of sig bits of double is 52 bits -> 4.5035996e+15 -> 15 decimal digits
- double is about 2x more precise
- single precision arithmetic is faster
Sources
- https://stackoverflow.com/questions/2835278/what-is-a-bias-value-of-floating-point-numbers
- https://www.log2base2.com/storage/how-float-values-are-stored-in-memory.html
- https://www.youtube.com/watch?v=aE2kVS0O0OE (special numbers)
- https://www.youtube.com/watch?v=WZUPNXsusOA (denorms)