Problem Statement

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

Each node in the graph belongs to exactly one group. For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1. Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

Example 1: 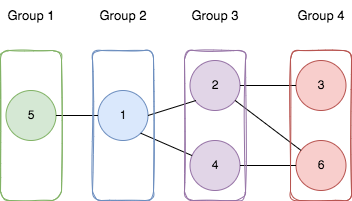Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]] Output: 4 Explanation: As shown in the image we:

Add node 5 to the first group.
Add node 1 to the second group.
Add nodes 2 and 4 to the third group.
Add nodes 3 and 6 to the fourth group. We can see that every edge is satisfied. It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Intuition

A valid graph that meets both of the conditions has to be a bipartite
The max number of groups is equal to maximum distance between two nodes in a graph

Approach

create an adjacency matrix
find minimum distance between nodes
iterate from 1 to n
- skip if the node has already been visited
- check if the graph this node is in qualifies to be a bipartite
- get max distance that can be found in this graph and add that to the answer

Code

Original Solution

    int bfs(unordered_map<int,vector<int>> & adj, int s) {
        queue<int> q;
        q.push(s);
        int depth = 0;
        unordered_set<int> visited;
        visited.insert(s);
        while (!q.empty()) {
            int size = q.size();
            unordered_set<int> neighbors;
            for (int i = 0; i < size; ++i) {
                int node = q.front();
                neighbors.insert(node);
                q.pop();
                for (int child: adj[node]) {
                    if (neighbors.find(child) != neighbors.end()) return -1;
                    if (visited.find(child) != visited.end()) continue;
                    visited.insert(child);
                    q.push(child);
                }
            }
            ++depth;
        }
        return depth;
    }
    void getGroups(int n, unordered_map<int, vector<int>> & adj, vector<vector<int>> & groups) {
        unordered_set<int> visited;
        for (int i = 1; i <= n; ++i) {
            if (visited.find(i) != visited.end()) continue;
            visited.insert(i);
            queue<int> q;
            vector<int> group;
            q.push(i);
            while (!q.empty()) {
                int node = q.front();
                q.pop();
                group.push_back(node);
                for (int nei: adj[node]) {
                    if (visited.find(nei) != visited.end()) continue;
                    visited.insert(nei);
                    q.push(nei);
                }
            }
            groups.push_back(group);
        }
    }
    int magnificentSets(int n, vector<vector<int>>& edges) {
        unordered_map<int, vector<int>> adj;
        for (vector<int> & e: edges) {
            adj[e[0]].push_back(e[1]);
            adj[e[1]].push_back(e[0]);
        }
        vector<vector<int>> groups; 
        getGroups(n, adj, groups);
        int global_max = 0;
        for (vector<int> & group: groups) {
            int local_max = INT_MIN;
            for (int member: group) {
                local_max = max(local_max, bfs(adj, member));
            }
            if (local_max == -1) return -1;
            global_max += local_max;
        }

        return global_max;
    }

Efficient Solution

    vector<int>adj[505];
    int col[505];
    int dis[505][505];
    bool flag;
    //nodes in a connected graph.
    vector<int>kara;
    
    //check if graph is bipartite
    void dfs(int u,int c=1){
        col[u] = c;
        kara.push_back(u);
        for(int&v:adj[u]){
            if(!col[v]) dfs(v,3-c);
            else if(col[v]==c)flag = 0;// graph is not bipartite
        }
    }
    //calculate minimum distance between all nodes.
    void bfs(int src){
        for(int i=1;i<=500;i++)dis[src][i] = 100001;
        dis[src][src] = 1;
        queue<int>q;
        q.push(src);
        while(q.size()){
            auto u = q.front();
            q.pop();
            for(int&v:adj[u]){
                if(dis[src][v]>dis[src][u]+1){
                    dis[src][v] = dis[src][u]+1;
                    q.push(v);
                }
            }
        }
    }
    int magnificentSets(int n, vector<vector<int>>& edges) {
        for(int i=1;i<=n;i++)adj[i].clear();
        memset(col,0,sizeof col);
        for(auto&e:edges){
            adj[e[0]].push_back(e[1]);
            adj[e[1]].push_back(e[0]);
        }
        
        for(int i=1;i<=n;i++)bfs(i);
        int ans = 0;
        int in = 0;
        for(int i=1;i<=n;i++){
            if(col[i]==0){
                kara.clear();
                flag = 1;
                in++;
                dfs(i);
                if(!flag) return -1;
                int mxdis = 0;
                for(int&i:kara){
                        for(int&j:kara){
                            mxdis=max(mxdis,dis[i][j]);
                        }
                }
                ans+=mxdis;
            }
        }
        return ans;
    }