Problem Statement

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of n cities numbered from 0 to n - 1 and exactly n - 1 roads. The capital city is city 0. You are given a 2D integer array roads where roads[i] = [ai, bi] denotes that there exists a bidirectional road connecting cities ai and bi. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer seats that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return the minimum number of liters of fuel to reach the capital city.

Example 1: 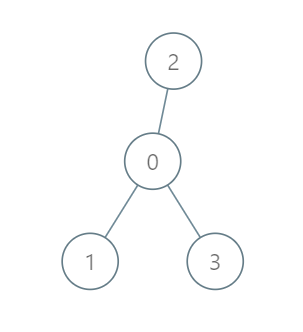Input: roads = [[0,1],[0,2],[0,3]], seats = 5 Output: 3 Explanation:

• Representative1 goes directly to the capital with 1 liter of fuel.
• Representative2 goes directly to the capital with 1 liter of fuel.
• Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed.

Intuition

We need to figure out how many passengers need to pass through a given city. Once we have that we know how many liters we need to move those passengers to the next city.

Approach

DFS

1. Create an Adjancency matrix using roads
2. Call dfs function (start at city 0) -This dfs function will try to return the number of passengers that need to travel from a given city
   • iterate through children city and retrieve how many passengers need to travel from cur_city
   • The number of liters required to move those people is passengers / seats = number of cars + if passengers / seats has any remainders, we need to add 1 to the number of cars
   • After calculating the above, we need to add it to the answer

Complexity

• Time complexity: O(n)
• Space complexity: O(n)

Code

class Solution {
public:
    long long dfs(unordered_map<int, vector<int>> & adj, int cur_city, int prev_city, int seats, long long & answer) {
        long long passengers = 1;
        for (int next_city: adj[cur_city]) {
            if (next_city == prev_city) continue;
            passengers += dfs(adj, next_city, cur_city, seats, answer);
        }
        if (cur_city) answer += passengers / seats + ((passengers % seats) ? 1 : 0);
        return passengers;
    }
    long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
        unordered_map<int, vector<int>> adj;
        for (auto & r: roads) {
            adj[r[0]].push_back(r[1]);
            adj[r[1]].push_back(r[0]);
        }
        long long answer = 0;
        dfs(adj, 0, -1, seats, answer);
        return answer;
    }
};