Problem Statement

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example 1: 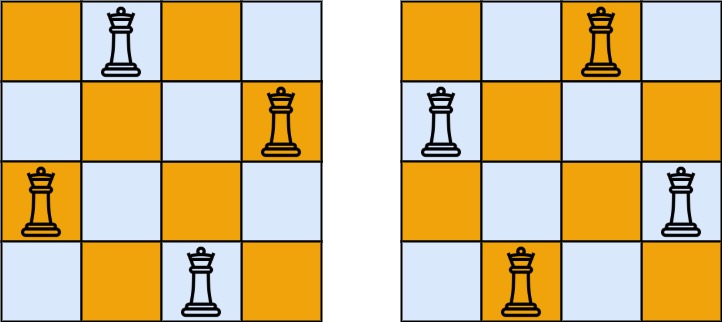Input: n = 4 Output: 2 Explanation: There are two distinct solutions to the 4-queens puzzle as shown.

Intuition

• Because we have to place N queens, we need to place at least one queen at each row. If we do not this, this will lead another row to have two queens which should be avoided
• Using the information above we can use recursion to get all the possible combinations. Now we need to figure out how we know if a queen at the given row does not interfere with other queens in the previous rows
• There are 3 ways a queen can advance; vertical, horizontal, diagonal. But using 1. we are making sure that none of other queens are on the same horizontal line.
• To check vertical lines, we can just add a datastructure (vector/set) that keeps track of all the column values of queens that have already been placed
• We are left with diagonal and antidiagonal.
  • For diagonal, let’s say a queen was placed in col 3 in the previous row and we are checking for col 2 for the current row. We can see that while row has increased, col has decreased. For it to create a diagonal line, the value of col + row needs to stay the same
  • For antidiagonal, we can see that as row increases, col also needs to increase by the same amount so the different between row and col stays the same

Approach

1. create datastructures to store col, diag, antidiag
2. cal recursion funtion which will return the count

Recursion function

1. The recursion function will has the current row as its argument and it will return once it reaches n;
2. For the given row we need to check for each column
   • check column
   • check if row + col already exist in diag
   • check if row - col + n - 1(n - 1 used to avoid neg numbers) exist in antidiag
3. If valid, update col, diag, antidiag and recur
4. After returning from recursion call, update col, diag, antidiag again to make them ready for next iteration

Complexity

• Time complexity: O(n ^ 2)

Code

    int totalNQueens(int n) {
        vector<bool> col(n), diag(2*n-1), anti_diag(2*n-1);
        return solve(col, diag, anti_diag, 0);
    }
   
    int solve(vector<bool>& col, vector<bool>& diag, vector<bool>& anti_diag, int row) {
        int n = size(col), count = 0;
        if(row == n) return 1;
        for(int column = 0; column < n; column++)           
            if(!col[column] && !diag[row + column] && !anti_diag[row - column + n - 1]){ 
                col[column] = diag[row + column] = anti_diag[row - column + n - 1] = true;
                count += solve(col, diag, anti_diag, row + 1); 
                col[column] = diag[row + column] = anti_diag[row - column + n - 1] = false; 
            }                                
        return count;
    }