Problem Statement

You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.

We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:

nums1[i] == nums2[j], and the line we draw does not intersect any other connecting (non-horizontal) line. Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).

Return the maximum number of connecting lines we can draw in this way.

Example 1: 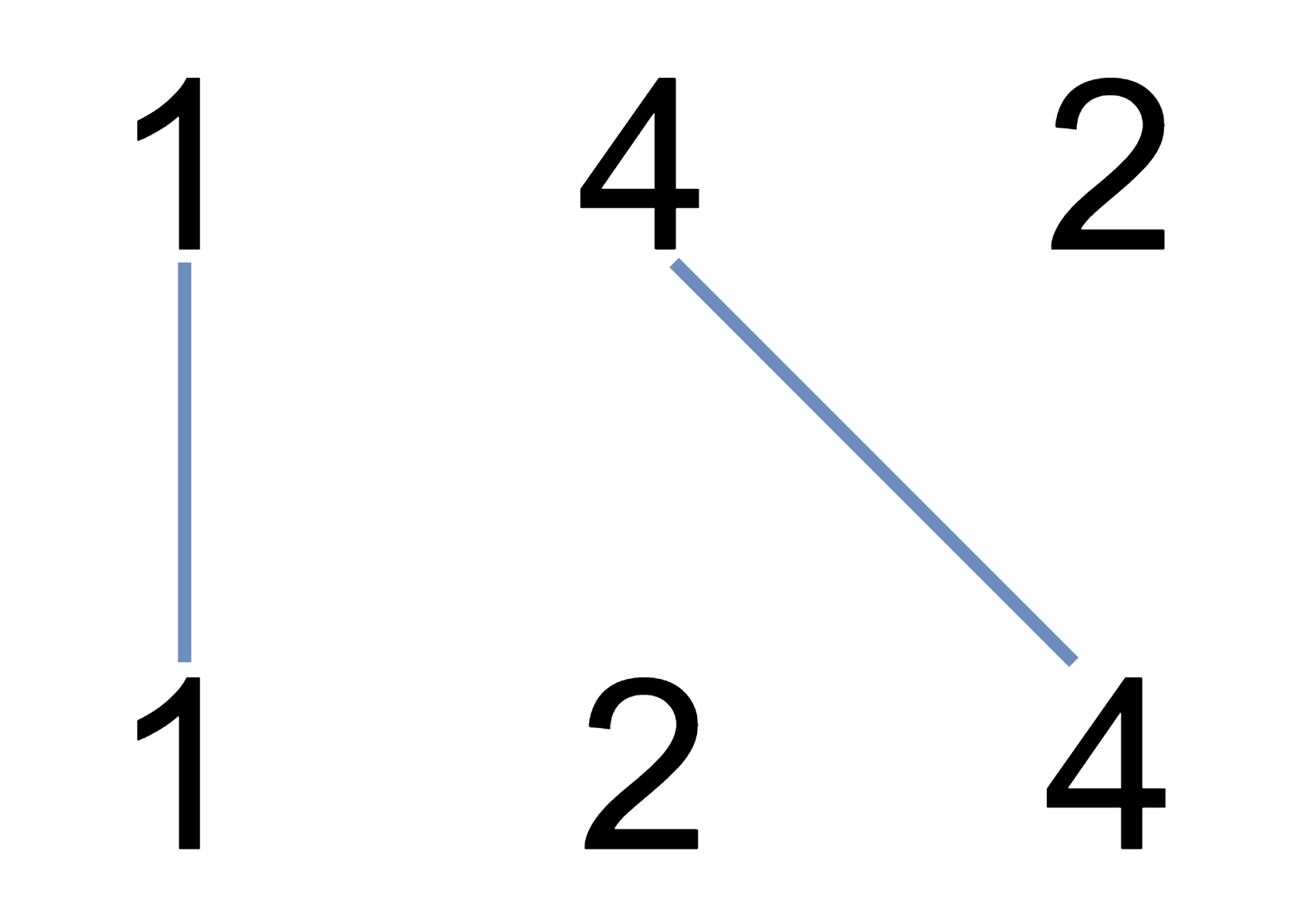Input: nums1 = [1,4,2], nums2 = [1,2,4] Output: 2 Explanation: We can draw 2 uncrossed lines as in the diagram. We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.

Intuition

• This problem is identical to Longest Common Subsequence problem
• line == common character

Approach

1. create 2d vector
2. do a nested for loop
   • when nums1[i] == nums2[j], 1 + dp[i - 1][j - 1]
   • when nums1[i] != nums2[j], max(dp[i - 1][j], dp[i][j - 1])
3. return dp[m][n]

Complexity

• space complexity: O(MN)
• time complexity: O(MN)

Code

    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                dp[i][j] = (nums1[i - 1] == nums2[j - 1]) ? 1 + dp[i - 1][j - 1] : max(dp[i][j - 1], dp[i - 1][j]);
            }
        }
        return dp[m][n];
    }